Genetic algorithms for under-identified models
Give up on “the one”
Agent-based models encode counter-factual mechanisms. Estimation/calibration/parametrization tries to divine counter-factual behaviour from factual-only observations (data). It is hard to believe that this would ever work, yet in almost all work on calibrating ABMs we implicitly assume so.
That is we look for the “best” fit (with some additional sensitivity analysis) rather than for the more informative set of all “good enough” fits.
I was therefore very happy to read a new paper on Environmental Modelling & Software by Williams precisely on this topic:
Williams, T. G., Guikema, S. D., Brown, D. G., & Agrawal, A. (2020). Assessing model equifinality for robust policy analysis in complex socio-environmental systems. Environmental Modelling and Software, 134, 104831. https://doi.org/10.1016/j.envsoft.2020.104831
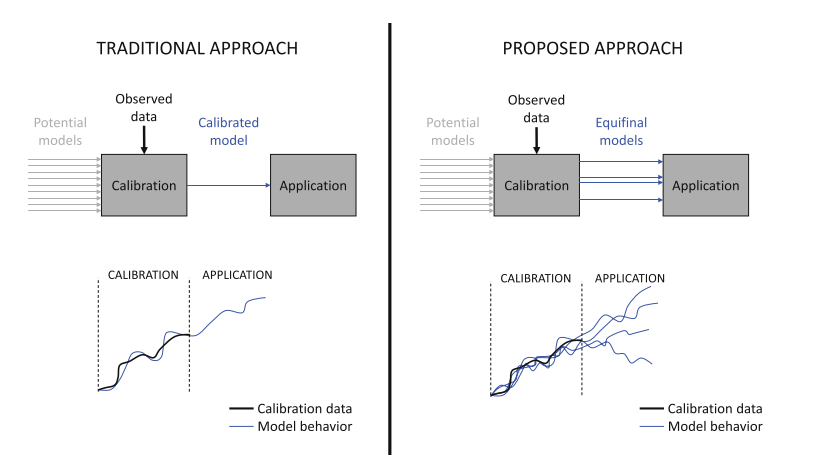
The idea itself is simple: use a genetic algorithm to reduce the distance between model output and “summary statistics” but target also “diversity” of solutions to keep the algorithm from collapsing on a single local maximum. Eventually grab some of the best performing parametrization and use them as a set of “good enough” model instances. When policy analysis comes, simulate it on all accepted parametrization to get a decent idea of what you have actually identified or not.
This is of course all music to my ears and the paper focuses quite well on this point. There are a few technical points that I think are a bit muddled and I think the paper make one fatal over-reach when presenting its results but I suggest everyone to read it!
The genetic algorithm step
The key technical suggestion of this paper is to calibrate models with a multi-objective genetic algorithm, with separate populations and a tournament selection that break ties through diversity.
The authors provide the code in python.
I think it’s a bit of a shame to focus so much of the paper on this step. There are a lot of GA variants that deal with niching and I wonder wether there is any benefit in having to code another one. Perhaps there aren’t that many options in python? Cluster-based GA, for example, is now almost 20 years old and doesn’t ask me to set the number of meta-populations in advance; can I use that one instead?
Matter of factly, I kept wondering if a non-GA solution would have worked as well (surely we can look at meta-models to look for multiple peaks, right?)
On the other hand, genetic algorithms are cool.
There is also the usual problem on how to weigh multiple summary statistics in the fitness function. This matters more here since weights help determine what is “good enough”. My feeling here is that we are better off imitating the “rejection filtering” literature and establish a priori what is the acceptable spread for each summary statistic rather than hide behind obscure weights. Either that or use regressions like in semiauto-ABC.
The robust policy step
A bad practice in environmental models, in my opinion, is dealing with uncertainty by splitting parametrization between the “policy” run and the “robustness” runs; the first we desperately believe in, the others are only there for some sensitivity test, and even that only begrudgingly so.
Therefore I really like the stance here in this paper: you can’t pick and choose, you have to look at the whole set and look and what is true for all or in aggregate.
I do think however that the plots can be quite misleading. When showing policy predictions the authors plot a full confidence interval with a boded median:
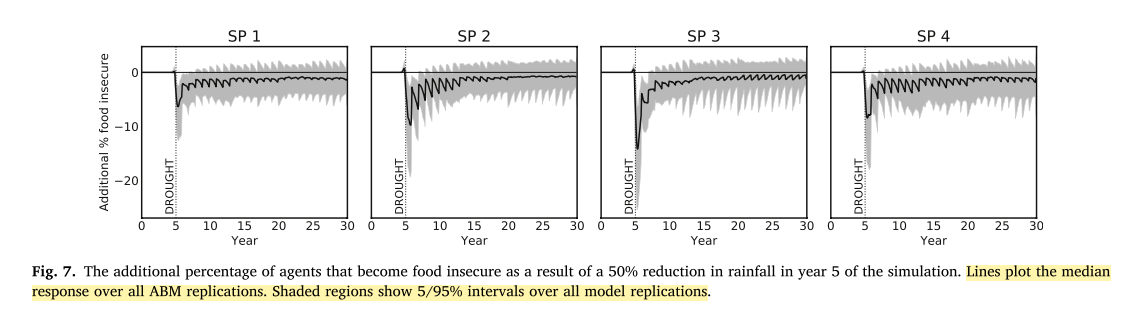
This seems quite wrong and an over-reach. What the genetic algorithm gives us is a diverse sample of parametrization that is good enough, but this plot seems to suggest that the sample is representative which it surely is not.
There is little point in highlighting a median and even worse cutting off the extreme predictions if we don’t know the probabilistic “weight” of each parametrization. There is an assumption in this graph that each of the parametrization found by the GA is “equally likely” to be correct for which no proof is provided.
The holy grail of under-identified models
We can generate a set of valid parametrization, but what can we do with it?
To me there seems to only ever be three ways to move on:
- We add Bayesian priors, reverting to Approximate Bayesian Computation which lulls us into thinking that the our parametrization set is actually representative (but good luck with believing those priors and goodbye to genetic algorithms)
- We cluster the set of parametrization into a few sub-groups, call these scenarios and revert back to “deep uncertainty” methods (that is, scenario based planning)
- Trust only results that are unanimous for all parametrization (super-robust?)
What’s missing here is something that would turn the results of any arbitrary GA search into a representative sample of sorts. That would be the holy grail for this kind of research. I am not even sure if it is possible (maybe a meta-model to do importance weighing like “arg-max oracle”(AMO) in contextual bandit algorithms?).
That seems to me to be the challenge of the near future for the field.